レポート/メールマガジン
REPORTS
プロがまとめた調査・考察レポートを無料公開中
レポート/メールマガジン
No.
14
企業価値評価における諸変数の合理的な範囲とは (1)
要 旨
➢企業価値評価の手法として最も一般的に用いられるDCF法においては、事業計画、割引率、成長率などインプットされる変数の種類が多く、なおかつそれぞれの変数が相当程度の見積もりの幅をもつために、評価者によって全く異なる結果が算出される場合がある。
➢カルチュア・コンビニエンス・クラブのMBOなど、売り手側と買い手側の算出した価格が異なる中で、株主自身が応募の意思決定を迫られる事案が出てきており、算定結果の見積もりの幅がどのようにして生じるかについて理解することが重要になると考えられる。
➢割引率は、事業計画と並んで算定結果に重要な影響を及ぼす要素の一つである。
➢割引率の構成要素の中でも、株主資本コストに関する見積もりの幅は大きく、特にエクイティ・リスクプレミアム、追加リスクプレミアムなどの見積もりで大幅な違いが生じることがある。
➢根拠のない追加リスクプレミアムの使用は裁判でも認められておらず、安易な使用には注意する必要がある。
はじめに
M&Aの価格交渉や、反対株主からの買取請求の裁判では、それぞれの当事者が全く違う価格を主張するということがよくあります。
直近の事例として、さる2月3日に発表されたカルチュア・コンビニエンス・クラブの経営陣による自社株買収(MBO)目的での公開買付けがあります。本件においては、公開買付者、取締役会、取締役会の委嘱を受けた独立委員会が、それぞれ独自に第三者算定機関を選定し、以下のような算定結果を入手しました。
<第三者算定機関の算定結果>
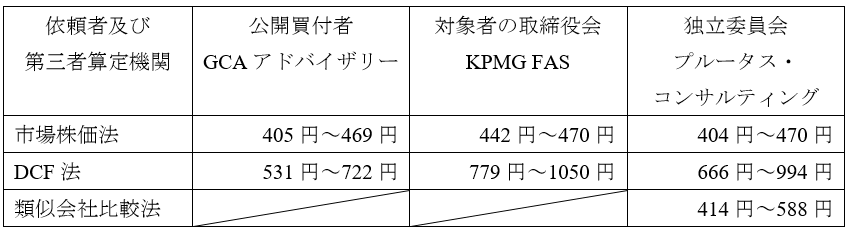
公開買付者は、公開買付価格として当初575円を提示したのに対し、独立委員会の第三者算定機関が提出した株式価値算定書においては、DCF法による算定結果の下限は666円となっていました。これを踏まえて、独立委員会と公開買付者との間で協議が行われた結果、公開買付価格は600円に引き上げられましたが、当該価格は依然として第三者算定機関の提出した算定結果の下限を下回る状況にありました。そのため、独立委員会は、本公開買付けを含む一連のMBOが将来の企業価値向上に資するものであり、本公開買付けに賛同意見を表明することには理由があるものの、公開買付価格が応募を推奨すべき水準には満たないとして、株主への応募の推奨に関しては中立の立場をとるのが相当との答申を行い、取締役会もその判断に従いました。その結果、本事例は、対象者の取得した第三者評価に比べて公開買付価格が低いことを理由に、対象者の取締役会が公開買付けへの応募に関する判断を株主に委ねた珍しいケースとなりました。
従来の公開買付けやM&Aの事例では、買い手側、売り手側それぞれの第三者算定機関による算定結果が近接しており、両者の重複する範囲で価格決定がなされることが一般的でしたが、カルチュア・コンビニエンス・クラブの事例を契機として、当事者の価格交渉における第三者評価の重要性が高まるとともに、双方の提示する価格が乖離した状況で、株主が自ら価格の妥当性に関する判断を迫られる場面も出てくることが予想されます。
それでは、なぜ評価者によってこのような算定結果の乖離が生じるのでしょうか。その理由は、企業価値評価においてインプットされる変数の多さにあります。企業価値評価における変数の種類は、オプションなどデリバティブの評価に必要となる変数に比べると格段に多く、なおかつそれぞれの変数には見積もりの幅があります。よって、当事者の一方がそれぞれの変数について評価結果を高く(あるいは低く)するような見積もりを採用すれば、それらが積み重なることによって、大幅な違いが生じることになります。その見積もりが合理的な範囲内であれば、特段問題視されるべきことではありませんが、中には合理的な範囲を逸脱するような恣意的な見積もりが少なからず横行しているのも事実です。
本稿では、今回と次回の二回にわたり、企業価値評価においてインプットされる変数にはどのようなものがあるか、それぞれの変数についてどのような見積もりの幅が生じるかを明らかにするとともに、理論や公式の機械的、恣意的な適用による不適切な算定の事例を取り上げ、注目すべきポイントについて解説します。本稿をご一読いただければ、ともすればブラックボックスのように映りがちな算定書の中にどのような論点が潜んでいるかについて、ご理解いただく一助になるのではないかと思います。今回は、企業価値評価において事業計画と並んで算定結果に重要な影響を及ぼす要因の一つである割引率のうち、特に見積もりの幅が生じやすい株主資本コストについて検討します。
1. 企業価値の評価手法
1. 1 三つのアプローチ
企業価値の評価手法は、インカム・アプローチ、マーケット・アプローチ、ネットアセット・アプローチの三つに大別されます。それぞれの内容は以下の通りです。
・インカム・アプローチ
評価対象会社から期待される利益ないしキャッシュ・フローに基づいて価値を評価する手法です。将来の収益獲得能力を価値に反映させやすく、評価対象会社がもつ固有の価値を示すとされます。主な評価手法として、DCF法、モンテカルロDCF法、調整現在価値法等があります。最も理論的な評価アプローチであり、マーケット・アプローチと並んで一般的に用いられる評価アプローチです。
・マーケット・アプローチ
評価対象会社の市場株価の分析、類似会社や類似取引事例などとの比較によって価値を評価する手法です。市場において成立した価格や取引に基づく評価アプローチであり、市場の取引環境を反映するとともに、客観性に優れているとされます。主な評価手法として、市場株価法、類似会社比較法、類似取引比較法等があります。最も客観性が高いことから、上場会社の評価においてほぼ例外なく採用される評価アプローチです。
・ネットアセット・アプローチ
主として評価対象会社の貸借対照表上の純資産に着目した手法です。貸借対照表を基に評価する静態的な評価アプローチであり、客観性・確実性に優れているとされます。主な評価手法として、簿価純資産法、時価純資産法等があります。インカム・アプローチ、マーケット・アプローチと異なり、主として企業の静的価値を求める手法であり、継続企業の評価手法としては一般的には用いられません。
1. 2 インカム・アプローチで算定結果の幅が生じやすい理由
株式譲渡やM&A, 公開買付けなど取引目的の価格算定においては、インカム・アプローチ及びマーケット・アプローチを用いるのが一般的です。これらのうち、マーケット・アプローチの算定結果は、市場株価や、PER, PBR, EV/EBIT倍率など市場株価に基づく倍率に依存するため、評価者によって算定結果に大幅な違いが生じることはありません。
これに対し、インカム・アプローチは、事業計画、割引率、成長率、非事業資産の見積もりなど、インプットされる変数がマーケット・アプローチに比べて格段に多く、なおかつそれぞれの変数の見積もりに相当程度の幅が生じうるため、評価者の採用した見積もりに応じて算定結果が全く違ったものとなる場合があります。
以下では、インカム・アプローチの中でも最も一般的に用いられるDCF法において、事業計画と並んで算定結果に重要な影響を及ぼす要素の一つである割引率を例に、どのような見積もり要素が存在するか、それぞれの見積もりの幅がどの程度に及ぶかなどについて明らかにします。
2. 割引率の役割とDCF法の概要
2. 1 割引率の役割
そもそも、割引率はなぜ必要になるのでしょうか。結論からいえば、割引率の役割は二つあります。一つは、貨幣の時間価値を反映することであり、もう一つの役割は、投資家の期待リターンを反映することです。
2. 1. 1 貨幣の時間価値の反映
あらゆる金融商品の価値は、それを保有することでもたらされる将来のキャッシュ・フローに依存して決まるというのがファイナンスの大原則です。ただし、現在の貨幣価値と将来の貨幣価値は同一ではありません。例えば、銀行に預金をすると、わずかとはいえ利子が付きます。このとき、現在の100円は将来において100円以上の価値をもちます。このように、時間の経過の経過とともに変化する貨幣の価値を、貨幣の時間価値といいます。
貨幣の時間価値を考慮する場合、異時点の貨幣価値を同一のスケールで測るため、将来のキャッシュ・フローを現在のキャッシュ・フローで測った価値に換算する(すなわち現在価値に割り引く)か、現在及び将来の各時点のキャッシュ・フローを、将来の一時点の価値に換算する(すなわち将来価値に割り戻す)必要があります。つまり、割引率は将来のキャッシュ・フローを現在価値へ割り引く換算レートということになります。
2. 1. 2 投資家の期待リターンの反映
将来のキャッシュ・フローを現在のキャッシュ・フローの価値で測るために割引率が必要となることは分かりましたが、次に問題となるのはどれだけのレートで割り引くかです。
この点、投資家の期待リターンが高ければ高いほど、将来のキャッシュ・フローの価値は現在のキャッシュ・フローの価値に比べて相対的に高くなります。例えば、投資家が年率10%のリターンを期待しているとします。このとき、実際のリターンが年率10%でなければ、投資家は目的を実現することができません。言い換えると、実際のリターンが10%未満のとき、投資家にはロスが発生します。このような関係を割引計算に反省させるためには、期待リターンの10%で将来のキャッシュ・フローを現在価値に割り引きます。そうすることで、実際のリターンが年率10%を上回れば(下回れば)投資家にはゲインが(ロスが)発生するという関係を適切に表すことができます。したがって、現在と将来のキャッシュ・フローと同じスケールで測るためには、投資家の期待リターンを反映したレートで割り引く必要があります。
ここで、期待リターンは、リスクの負担と引換えに投資家が要求するものであることからすると、割引率は投資家の期待リターンを反映すると同時に、割り引かれるキャッシュ・フローのリスクを織り込んだものということもできます。
2. 2 割引率の構成要素
2. 2. 1 WACCの構成要素
DCF法において一般的に用いられる加重平均資本コスト(Weighted Average Cost of Capital; WACC)を前提とした場合、割引率は以下のように表されます。
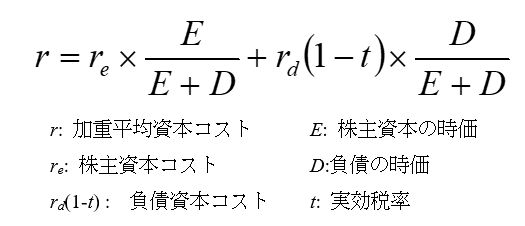
よって、割引率は株主資本コストと負債資本コストを、株主資本比率及び負債比率で加重平均することによって求められます。株主資本コストは、さらにいくつかの計算要素に分かれます。それを次項で見て行きましょう。
2. 3. 2 株主資本コストの構成要素
株主資本コストの算定方法にはいくつかの方法があります。最も一般的に用いられるのは、以下の式で示される資本資産評価モデル(Capital Asset Pricing Model; CAPM)です。
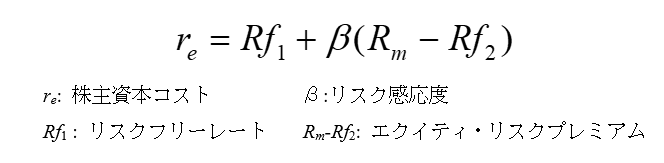
一般に、株主資本コストは、安全性の高い長期債券の利回り(リスクフリーレート)に超過リターンを上乗せしたものとして算定されます。CAPMはこのような考え方に基づく推計モデルの一つで、エクイティ・リスクプレミアムという単一のリスクファクターと、それに対する感応度であるβをかけ合わせることによって超過リターンを求めるという点に特徴があります。この他、3種類のリスクファクターを想定するFama-Frenchの3ファクターモデルや、多数のリスクファクターを想定するマルチファクターモデルなどが知られていますが、リスクファクターが単一という扱いやすさや、現代ポートフォリオ理論を背景とした理論的な一貫性の高さから、実務上はCAPMの利用が主流となっています。
なお、本来のCAPMにおいては、リスクフリーレート、β, エクイティ・リスクプレミアム以外の変数は想定されていませんが、CAPMで説明できない超過リターンを考慮するため、実務上は追加的なリスクプレミアムを考慮する場合があります。この場合、株主資本コストは以下のように表されます。
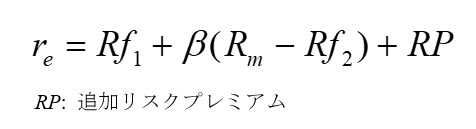
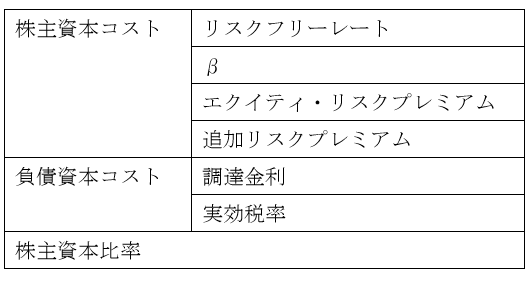
以上をまとめると、割引率は以下のような構成要素に分類できることになります。これらのうち、リスクフリーレートと負債資本コストについては、評価者によって違いが生じることは少なく、仮に違いが出たとしても重要な影響はありません。しかし、それ以外の要素については評価結果に少なからぬインパクトを与えることが多く、恣意的に選択されれば評価結果を歪めることにもなりかねません。以下では、それぞれの構成要素ごとに、見積もりの方法と見積もりの幅が出る要因について見て行きます。
3. 株主資本コスト
3. 1 リスクフリーレート
3. 1. 1 「リスクフリー」とは何か
リスクフリーレートとは、デフォルトリスクがない証券の利回り、具体的には長期国債の利回りを意味します。
3. 1. 2 短期金利と長期金利のいずれを使うか
理論上は、キャッシュ・フローの発生時期に一致する期間の金利を用います。しかし、DCF法においては半永久的にキャッシュ・フローを割り引くのが通常であり、それぞれの時点における割引率を求めるのは困難です。そこで、実務上は単純化のため一定の長期金利を用います。
3. 1. 3 長期金利は長期であるほど望ましいか
半永久的な長期間のキャッシュ・フローを現在価値へ割り引くには、可能な限り長い期間の金利を用いるべきとも考えられます。しかし、超長期の債権は流動性が低く、利回りにプレミアムが上乗せされている可能性があり、リスクフリーレートとしては適切ではありません。また、キャッシュ・フローの発生時点が将来になればなるほど、現在価値に与えるインパクトが低くなることを考えると、長期の金利であるほど望ましいとはいえません。そのため、実務上は最も流動性の高い10年国債の利回りを用いるのが一般的となっています。
3. 1. 4 現在値と平均値のいずれを使うか
リスクフリーレートの見積もりについて、唯一誤りが生じやすいのが、リスクフリーレートの現在値と過去の平均値のいずれを用いるかという問題です。結論からいいますと、リスクフリーレートが将来のキャッシュ・フローを現在価値に割り引く基礎となるレートであることからすると、過去値ではなく現在値を用いるのが合理的です。
この点、短期的な金利の変動を排除するため平均値の方が望ましいという見解もないわけではありません。しかし、リスクフリーレートのボラティリティは株価に比べて非常に低く、長期間のデータの平均により誤差を小さくする意義はあまりありません。
3. 1. 5 リスクフリーレートの合理的な範囲
以上のように、リスクフリーレートの見積もりに関しては、10年国債の現在値を用いるということでほぼ確立しており、評価者によって差が出ることはまずありません。見方を変えると、これ以外の見積もりが採用されているとすれば、上記の点に関する誤解がなされているか、割引率を恣意的に操作する目的でなされている可能性が高いと推測することができます。
3. 2 β
3. 2. 1 βとは何か
βは、エクイティ・リスクプレミアムに対する感応度で、エクイティ・リスクプレミアムは、株式市場の超過リターンです。一般に用いられるヒストリカルβは、過去の一定期間における株価指数の変化率を説明変数、ある株式の株価の変化率を被説明変数として、回帰分析を行うことにより算出されます。βが1より低ければ(高ければ)、市場平均よりリスクが低い(高い)というのが「直観的な」説明です。ただし、「リスク」の内容については留意すべき点があります。この点につき次項で説明します。
3. 2. 2 βで表されるリスク
CAPMにおいては、全ての株式のリスクはβとエクイティ・リスクプレミアムの積で表されます。このような結果が導かれる背景には、現代ポートフォリオ理論が存在しています。現代ポートフォリオ理論の詳細は割愛しますが、その中核となる概念の一つが「分散投資」です。投資家が様々な銘柄に分散投資をすることにより、それぞれを単独で保有した場合に比べてリスクが減殺される結果、市場均衡において代表的な投資家が保有するポートフォリオ(マーケット・ポートフォリオ)には、景気変動や金利、為替の影響など、分散投資で回避できない市場全体に共通するリスク(システマティック・リスク)だけが残り、そのリスクに応じた超過リターンがエクイティ・リスクプレミアムとして表されるものとされます。そして、市場に存在する個々の証券の超過リターンは、エクイティ・リスクプレミアムに対する感応度、すなわちβの大小に応じて決まるというのがCAPMの骨子です。したがって、分散投資で解消しうる企業固有のリスク(アンシステマティック・リスク)はβに反映されておらず、システマティック・リスクのみが反映されているということになります。
このことを示しているのが、βを導く以下の算式です。
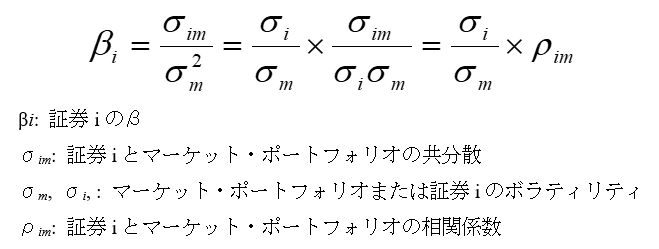
上記の通り、βは「個別銘柄とマーケット・ポートフォリオの標準偏差の比」と、「個別銘柄とマーケット・ポートフォリオのリターンの相関係数」の二つに分けられます。前者はマーケット・ポートフォリオのリスク1単位当たりで測った個別銘柄のトータルリスクの大きさであり、分散投資によって解消できるアンシステマティック・リスクと、解消できないシステマティック・リスクの両方を含んでいます。これに対して、後者はシステマティック・リスクがトータルリスクの中に占める割合と解釈できます。以上の関係からすると、銘柄のトータルリスクが高く(低く)とも、マーケットとの相関関係が低い(高い)銘柄については、システマティック・リスクの割合が低く(高く)、βは相対的に低く(高く)なります。したがって、βは単なるリスクの尺度ではなく、システマティック・リスクの尺度と解釈できます。
3. 2. 3 βの合理的な範囲
以下の図表は、昨年12月の時点において、国内の株式市場に上場している全ての国内企業のβを算出し、その分布を示したものです。7割以上の企業のβが1以下となっています。
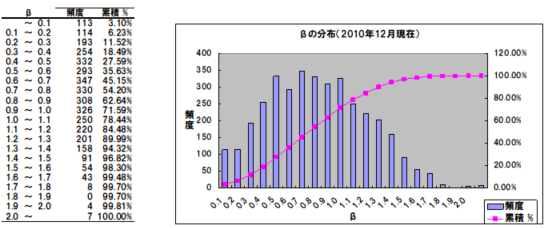
3. 2. 1では、βが1より大きい(小さい)と市場平均よりリスクが高い(低い)と述べました。このことからすると、βが1より大きい企業と1より小さい企業がそれぞれ同数ずつ存在するかのようですが、実際には70%以上の企業でβが1以下となっています。その理由は、ここでいう「市場平均」が加重平均を指しているからです。
以下の表は、同じ母集団を時価総額の低い順に10段階の階級に分け、それぞれにおけるβの平均を求めたものです。この表からは、時価総額の階級が上がるとβも高くなる傾向が、一部を除いて成立しているということにお気づきいただけるかと思います。
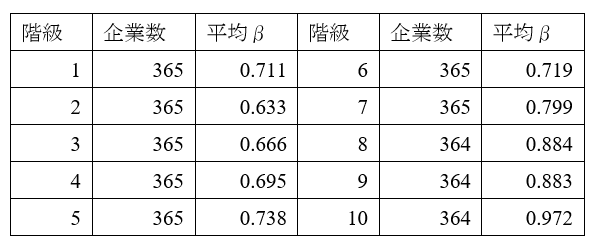
このような関係が成立するのは、ある株式の時価総額が高くなればなるほど、それ自体が市場全体に与えるインパクトが大きくなり、システマティック・リスクが高くなるという理由によります。したがって、βを加重平均した場合、時価総額の高い階級の高いβのウェイトが大きくなり、平均が1に近づきます。
少し脱線しましたが、再度βの度数分布をご覧下さい。βは、0.4から1.1の範囲に全体の約60%, 0.3から1.3の範囲に全体の約80%, 0.2から1.4の範囲に全体の約90%が含まれていることが分かります。言い換えると、0.2未満や1.4を超えるようなβは異常である可能性が少なくないということです。特に、1.5を超えるβが全体の3%未満であることを考えると、このような水準のβが評価に使われている場合には、何らかの操作が加えられている可能性が疑われます。
3. 3 エクイティ・リスクプレミアム
3. 3. 1 エクイティ・リスクプレミアムの算出方法
エクイティ・リスクプレミアムは、算出方法の違いにより、ヒストリカル・リスクプレミアムとインプライド・リスクプレミアムに分けることができます。
3. 3. 1. 1 ヒストリカル・リスクプレミアム
過去の株式市場における超過リターンを平均することによって求められるリスクプレミアムをいいます。過去のリターンを平均するのは、株式市場の短期的な変動の影響を取り除いた長期的な動向を反映させるためで、このような観点から、平均値を求める期間は長期であることが望ましいとされます。平均値の求め方には単純平均と幾何平均があり、統計的な誤差を平準化する観点からは前者が、複利の年平均利回りを求める観点からは後者が適合します。実務上は、わかりやすさと統計学的な扱いやすさから、単純平均を用いるのが一般的です。
3. 3. 1. 2 インプライド・リスクプレミアム
株式市場の期待リターンと株価の関係を定式化するモデルから逆算されるリスクプレミアムをいいます。例えば、仮に企業が公表している予想利益が永続するものとして株価が形成されていると仮定します。このとき、予想利益と株価の間に「株式時価総額=予想利益÷ROE」という関係が成り立ちます。これを整理すると、「ROE=予想利益÷株式時価総額」と表すことができます。このようにして求めたROEからリスクフリーレートを差し引くことにより、その株式の超過リターンが算出できます。これをインプライド・リスクプレミアムといいます。同様の手続により全ての企業のインプライド・リスクプレミアムを集計すれば、市場全体のインプライド・リスクプレミアムが算出できます。
3. 3. 2 それぞれの特徴と問題点
3. 3. 2. 1 ヒストリカル・リスクプレミアムの特徴と問題点
ヒストリカル・リスクプレミアムは市場において実際に観察されたリターンに基づくため客観性が高いといわれます。しかし、長期間の捉え方には幅があり、どの期間を選択するかで全く結果が異なります。以下の表は、昨年末を基準としたヒストリカル・リスクプレミアムが、観察期間によってどのように変わるかを示したものです。ヒストリカル・リスクプレミアムは、観察期間を短くするほど低くなっており、特に過去20年のヒストリカル・リスクプレミアムはマイナスになっています。これは、リスクフリーレートより株式のリターンが低いということであり、論理的に破綻しています。
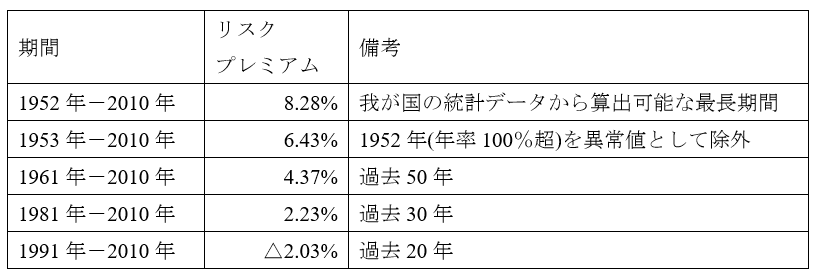
また、ヒストリカル・リスクプレミアムについては、投資家のリスク許容度が不変であることを前提とし、市場環境の変化に即応できないこと、長期間にわたるリターンが観測できる一部の安定した市場を観察することにより、リスクプレミアムの中にバイアスが介在することなども問題点として指摘されています。
3. 3. 2. 2 インプライド・リスクプレミアムの特徴と問題点
インプライド・リスクプレミアムには、観察期間の長短に依存せず、同一のモデルを継続適用する限り恣意性が介入しにくいという特徴があります。また、ヒストリカル・リスクプレミアムに比べ、市場環境の変化に即応しやすいという利点があります。すなわち、利益が一定で株価が下がれば(上がれば)、インプライド・リスクプレミアムは上昇(下落)するという関係が成り立ちます。しかし、期待リターンと株価の間にどのような関係を想定するかが確立しておらず、採用するモデルによって算出されるリスクプレミアムは異なります。
3. 3. 3 エクイティ・リスクプレミアムの合理的な範囲
株価算定書は非開示が原則であり、仮に開示される場合でも、割引率の算出過程まで明らかにされるものは皆無に等しい状況です。よって、実務上採用される一般的なリスクプレミアムの水準を具体的な数値で示すことはできません。よって、あくまで経験則に過ぎませんが、買取価格をめぐる裁判事例に関与し、他社の算定書を多数検証した限りでは、8割から9割方の事例でヒストリカル・リスクプレミアムが採用されており、平均値の算出期間としては30年から50年が用いられているように見受けられます。これには、客観性を担保しようとすると、明確な根拠があり、なおかつ実務において最も一般的に用いられているものを利用するのが最も適切であり、逆にそれ以外のものを採用しようとすると拠り所がなくなってしまうという背景があるものと思われます。ただし、バブル崩壊後の長期にわたる株式市場の低迷を考えると、ヒストリカル・リスクプレミアムが極端な場合マイナスになるといった事態も考えられないわけではなく、「ヒストリカル・リスクプレミアムを使っておけば安心」という安易な考えは早晩通用しなくなる可能性があります。
企業価値評価のテキストでは、以下の表のように4-6%程度の水準が「一般的な水準」として示されているものの、その根拠については経験則の域を出ておらず、明確な根拠を示しているものは皆無に等しい状況です。

この点につき、Ibbotson Associates Japan代表の山口勝業氏は、自らの著書「日本経済のリスクプレミアム」(東洋経済新報社)で、行動ファイナンスで用いられる「アンカリング」「ハーディング」という概念を例に、「一般的な」リスクプレミアムの水準が形成される理由を説明しています。「アンカリング」とは、ある参照点を示すと、予想や期待がその回りに形成されがちになるという現象で、エクイティ・リスクプレミアムに関しては、テキストで例示される「4-6%」という数字が参照点としての役割を果たしていることになります。また、「ハーディング」とは、自分が変わり者と思われないために無難な答え(ここでは4-6%)を指向するという現象をいいます。
以上のように、エクイティ・リスクプレミアムの水準について一致した見解はありません。例えば、弊社が公表している最新のインプライド・リスクプレミアムは約8%で、テキストにおいて「一般的」とされる水準に比べ相当程度高くなっています。しかし、エクイティ・リスクプレミアムに関する限り、「一般的」であることと「合理的」であることは必ずしも一致しないということに留意する必要があります。ただし、4-6%の水準を大きく超えるか、大きく下回るような見積もりがなされている場合には、その合理性について検証する意義があると考えられます。
3. 4 追加リスクプレミアム
3. 4. 1 追加リスクプレミアムはなぜ生じるか
完全に効率的な市場においては、分散投資を通じて全てのアンシステマティック・リスクが相殺され、リスクファクターはシステマティック・リスクに対応したエクイティ・リスクプレミアムに集約されます。また、個別企業のリスクは、エクイティ・リスクプレミアムに対する感応度であるβに集約されます。しかし、以下の理由により実際の株式市場は不完全であり、個別企業の超過リターンがCAPMで推計されるリターンから乖離する場合があります。このような乖離を説明するため、実務においては追加リスクプレミアムとして一定割合を株主資本コストに上乗せすることがあります。
・取引費用の存在
・取引単位の不可分性
・情報の非対称性
・株価の不連続的な変化
・税金の存在
・貸付金利と借入金利のスプレッド
3. 4. 2 追加リスクプレミアムは定量化可能か
完全市場ではエクイティ・リスクプレミアム以外のリスクファクターは存在しないはずであり、追加リスクプレミアムという概念は、CAPMの理論上の前提に相容れません。実際上も、理論値と実際のリターンとの乖離は様々な要因によって生じ得るものであり、いかなる原因によって乖離が生じたかを特定すること自体が困難です。実務上用いられている追加リスクプレミアム(非流動性リスク、計画未達リスク等)に理論的根拠は希薄であり、恣意的な操作の温床になっているのが現状です。
3. 4. 3 サイズ・リスクプレミアムの推計方法
追加リスクプレミアムの中で、時価総額の違いに応じた追加的なリスクプレミアム、いわゆるサイズ・リスクプレミアムについては、比較的客観的な定量化が行われています。最も広く知られているのは、米国企業の時価総額別ポートフォリオの超過収益を長期にわたって平均することにより求めたサイズ・リスクプレミアムです。ただし、我が国において対応する時価総額別ポートフォリオ時系列データは存在しておらず、時価総額の分布が大きく異なる米国企業のデータを準用せざるを得ないのが現状となっています。
3. 4. 4 サイズ・リスクプレミアム利用上の留意点
米国の株式市場のデータを利用する場合、我が国と平均リターンも時価総額の分布も異なる 市場のデータを利用するのが妥当かどうかという問題点があります。なぜなら、米国市場で時価総額2億ドルの企業は下位10%未満の階級に属するのに対し、我が国の通貨単位で同程度の規模をもつ時価総額160億円の企業は上位35%程度に属し、市場における相対的な位置が全く異なるからです。
また、CAPMが想定するリスクファクターはエクイティ・リスクプレミアムのみであり、それ以外のプレミアムを上乗せすることで、同じリスクを二重にカウントする可能性があります。すなわち、小型株のリスクは高いボラティリティの中に織り込まれ、βを高めていると考えれば、βとサイズ・リスクプレミアムで同じリスクを二重に計上することにもつながります。
そのため、サイズ・リスクプレミアムを使用するに際しては、小型株のリスクが含まれない(あるいは僅少)と考えられる、時価総額が大きく流動性の高い株式のβを使用する等の配慮が望ましいと考えます。逆に、これらの配慮がなされず、ただ機械的にプレミアムが加算されているに過ぎない場合には、合理的な算定とはいえない可能性が高くなります。
サイズ・リスクプレミアムの概念自体は知っていても、以上のような問題点を理解している評価者はきわめて少ないのが現状であり、「実務上一般的である」ということのみをもって機械的に適用することで、知らず知らずの間に誤った算定をしてしまっている例の最たるものがこのサイズ・リスクプレミアムです。特に反対株主からの買取請求等が予想されるようなセンシティブな事案においては、安易な追加リスクプレミアムの利用は慎むべきと考えます。
小括
次回は負債資本コスト、資本構成等、その他の主要な変数の見積もりについて解説するとともに、DCF法による評価の妥当性が裁判上争われたカネボウ事例を取り上げ、当事者の主張における見積もりの乖離と、それに関する裁判所の判断についてご説明します。
以上
M&A・組織再編のレポートを見る
-
はじめに 2025年7月22日、東京証券取引所(以下「東証」という。)による「MBOや支配株主による完全子会社化に関する上場制度の見直し等に係る有価証券上場規程等の一部改正」(以下「本改正」...
-
上場企業によるM&A投資基準策定の動き~コーポレートガバナンスコード改訂との関連~(2025年9月号)
はじめに 上場企業によるM&A投資資金枠にかかるIR開示事例が増加傾向にあります。当社グループの顧客企業からは、M&A強化の次の課題として、投資判断基準を定義したいとの声が多く聞かれるように...
-
海外会社の企業価値評価:DCF法における重要ポイント(2025年8月号)
はじめに 企業価値評価の目的は多岐にわたり、M&Aにおける事業や株式の取得・譲渡、グループ内再編、さらには財務報告でのれんの減損テストや株式持分の公正価値評価など、多くのご依頼をいただいてお...
-
公正なM&A指針公表後5年間における特別委員会/フェアネス・オピニオン実務の変化(2024年07月31日号)
Topic. ► 公正なM&A指針公表後5年間における特別委員会/フェア...
-
「資本コスト経営」の視点で読み解く継続価値(2024年5月31日号)
Topic. ► 「資本コスト経営」の視点で読み解く継続価値 ...
-
株式交付制度公表事例による株価算定手法分析等の追跡調査(2023年08月31日号)
Topic. ► 株式交付制度公表事例による株価算定手法分析等の追跡調査 ...



M&A・組織再編の事例を見る
-

養命酒製造株式会社の株式公開買付けにおける助言の提供及び株式価値の算定
養命酒製造株式会社(東証プライム 2540)による主力事業への経営資源集中を企図した事業再編手続きの一環として行われる、株式会社レノによる株式公開買付けに際し、養命酒製造株式会社が公正性担保のために設
続きを読む
-

JX金属株式会社と東邦チタニウム株式会社の株式交換における株式価値の算定及び意見表明
JX金属株式会社(東証プライム 5016)と東邦チタニウム株式会社(東証プライム 5727)の株式交換に際し、東邦チタニウム株式会社が公正性担保のために設置した特別委員会の第三者算定機関として株式価値
続きを読む
-

伊藤忠商事株式会社による伊藤忠食品株式会社の完全子会社化における助言の提供、株式価値の算定及び意見表明
伊藤忠商事株式会社(東証プライム 8001)が連結子会社である伊藤忠食品株式会社(東証プライム 2692)を完全子会社とするために行う株式公開買付けに際し、伊藤忠食品株式会社が公正性担保のために設置し
続きを読む
M&A・組織再編のソリューションを見る
-
株価算定
株価算定 エクイティファイナンス、M&A、TOB、自社株買いなど、株式や事業の譲渡、移転を伴う取引価格の決定、裁判における価格の立証、会計処理を前提とした評価額の算定など様々な目的に応じ、第
-
合併・株式交換・株式移転
合併・株式交換・株式移転 合併・株式交換・株式移転に際して株式価値を算定する場合、それぞれの企業の価値を別個に算定するときよりも、考慮すべき要素は多岐にわたります。これは、複数の企業を整合的な手法に
-
TOB
公開買付け(TOB、take-over bid) 一定数以上の上場株券等を買付ける目的で公開買付けを実施する場合には、公開買付届出書により通常の取引よりも厳格な情報開示が求められ、その範囲は公開買付
-
MBO
非公開化・MBO(Management Buyout) 抜本的な経営改革の手段として、MBOを含む非公開化が選択される場合、買手と少数株主の間に構造的な利益相反が存在することから、公正性の担保が重要
-
スクイーズアウト
スクイーズアウト 少数株主からの強制取得、いわゆるスクイーズアウトがなされる局面としては、非公開化・MBOの一環として行われる場合の他、取引先の非上場会社を完全子会社化する場合、分散した株式を創業家
-
債権譲渡
債権譲渡 グループ会社間取引やM&A取引において、金融債権が独立して譲渡される場合があります。 プルータス・コンサルティングの強み プルータスは、これまで培った豊富な評価経験及び金融債権

