リスクプレミアム再考 –単純平均型と加重平均型-｜企業価値評価・算定のプルータス・コンサルティング公式サイト

1. はじめに

先月のレポートでは、「サイズ・リスクプレミアム再考 –ヒストリカル手法とインプライド手法-」と題し、弊社が企業価値評価用データ配信サービス”Value Pro”で提供しているインプライド手法によるサイズ・リスクプレミアムの考え方を、従来から利用されてきたヒストリカル手法によるサイズ・リスクプレミアムと対比する形で述べました。
Value Proで提供しているインプライド手法によるリスクプレミアムは、マーケット・リスクプレミアムについてもサイズ・リスクプレミアムについても、集計対象となった企業の株式の超過収益率を単純平均することにより算出されています。これに対し、単純平均に代えて各企業の株式時価総額を基準とした加重平均を用いることも考えられます。本稿では、インプライド・リスクプレミアムとサイズ・リスクプレミアムに関し、従来から提供してきた「単純平均型」に加え、株式時価総額を基準とした「加重平均型」を導入し、集計結果がどのような影響を受けるかについて検討します。

2. 単純平均型のリスクプレミアム

まず、単純平均型のインプライド・リスクプレミアム及びサイズ・リスクプレミアムの算出方法の概要を下記にまとめました。

2. 1 インプライド・リスクプレミアム

インプライド・リスクプレミアムとは、資本資産評価モデル(CAPM)における変数の一つであるマーケット・リスクプレミアムを、企業の予想利益と株価の関係から逆算したものです。
インプライド・リスクプレミアムを求めるにあたっては、企業の予想利益と株価との間にどのような関係を想定するかが問題となります。Value Proでは、次式のように、企業の予想当期純利益が永続するという前提で株価が形成されるとの前提を置いています。

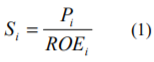
ここで、Siはある企業の株式時価総額、Piはその企業が公表している予想当期純利益、ROEiはその企業の株主資本コストを意味します。(1)式をROEiについて表すと次式のようになります。

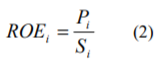
ここで、(2)式の左辺がCAPMにより表されるものとすると、次式のような関係が導かれます。

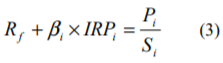
ここでRfはリスクフリーレート、βiはその企業の株式のリスク感応度、IRPiはその企業の株式のインプライド・リスクプレミアムです。リスクフリーレートとβiは市場のデータから算出できるため、これらが決まれば次式のようにインプライド・リスクプレミアムを求めることができます。

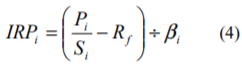
(4)式により求めた各企業の株式のインプライド・リスクプレミアムから、異常値を除外し平均することにより、市場全体のインプライド・リスクプレミアムが次式のように算定されます。

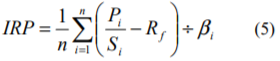
ここでIRPは、集計対象となった企業のインプライド・リスクプレミアムの平均値、nは企業の数を示しています。

2. 2 サイズ・リスクプレミアム

サイズ・リスクプレミアムとは、投資家が小型株に対して追加的なリスクプレミアムを要求するという前提に基づき、CAPMで推計される株主資本コストに加算されるリスクプレミアムです。

2. 2. 1 サイズ・リスクプレアムの算出過程

サイズ・リスクプレミアムの算出方法については、先月のレポートにも示しましたが、改めてまとめると以下のようになります。

2. 2. 1. 1 各企業の超過収益率の算出

ある企業の株式の超過収益率が、次式のように表されるものと仮定します。

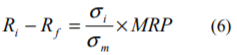
ここで、Ri-Rfはある企業の株式のリスクフリーレートに対する超過収益率、σiは当該企業の株式のボラティリティ、σmは全株式のボラティリティの平均値、MRPはマーケット・リスクプレミアムです。

2. 2. 1. 2 各階級の超過収益率の算出

我が国の株式市場に上場している国内企業を、時価総額別を基準として10階級に分け、各階級に属する企業の超過収益率を平均することにより、次式のようにそれぞれの階級の超過収益率を算出します。

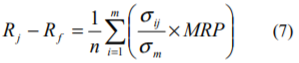
ここで、Rj-Rfは第j階級の超過収益率、nは各階級に属する企業の数、σijは第j階級に属する企業の株式のボラティリティを意味します。小型株のボラティリティは大型株に比べて一般に高いため、時価総額の低い階級では、(7)式を前提とした超過収益率も相対的に高くなります。

2. 2. 1. 3 サイズ・リスクプレミアムの算出

(7)式で算定されたある階級の超過収益率の平均値から、前提となったマーケット・リスクプレミアムを差し引くことにより、その階級のサイズ・リスクプレミアムが算出されます。

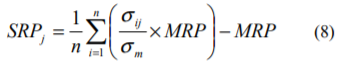
(8)式を整理すると次式のようになります。

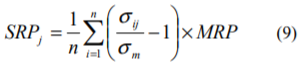
2. 2. 2 サイズ・リスクプレミアムの性質

サイズ・リスクプレミアムに関し、ご留意いただきたい点が三つあります。

2. 2. 2. 1 マーケット・リスクプレミアムに比例する

まず、(9)式から明らかなように、サイズ・リスクプレミアムはマーケット・リスクプレミアムに比例します。たとえば、マーケット・リスクプレミアムを6%と想定した場合のサイズ・リスクプレミアムは、全ての階級において、マーケット・リスクプレミアムを5%と想定した場合のサイズ・リスクプレミアムの1.2倍となります。

2. 2. 2. 2 ディスカウントが発生する階級もある

サイズ・リスクプレミアムといっても、全ての階級にプレミアムが発生するわけではありません。すなわち、大型株のボラティリティは、市場全体の平均よりも低い傾向があるため、時価総額が高い階級では、(9)式におけるボラティリティの比が1よりも小さくなる企業の割合が多くなります。その結果、SRPが負の値をとり、実質的にはディスカウントとなります。

2. 2. 2. 3 全階級のサイズ・リスクプレミアムの平均値は0となる

(9)式において、σmは全株式のボラティリティの平均値であることから、これを次式のよう表すことができます。

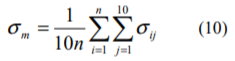
また、全階級のサイズ・リスクプレミアムを平均すると次式のようになります。

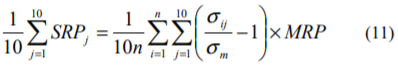
ここで、(10)式の関係に留意しつつ(11)式からσijを消去すると次式のようになります。

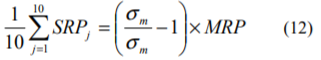
(12)の右辺の括弧内が0となることから、全階級のサイズ・リスクプレミアムの平均値が0となることが確かめられました。

3. 加重平均型のリスクプレミアム

基本的な考え方は単純平均型と同様ですが、平均値の算出に際して加重平均を用いる点が異なります。

3. 1 インプライド・リスクプレミアム

各企業の株式のインプライド・リスクプレミアムを算出する過程は単純平均型と同様ですが、異常値除外後の全企業の平均値を求めるにあたり、採用された企業の株式時価総額に基づく加重平均を用います。

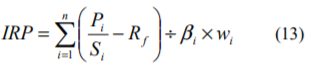
wiは、集計対象となった全企業の株式時価総額に占める、ある企業の株式時価総額の割合です。ここで、全企業の株式の時価総額をSとすると、wiを次式のように表すことができます。

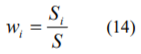
(14)式を(13)式に代入することにより、加重平均型のインプライド・リスクプレミアムは以下のように表されます。

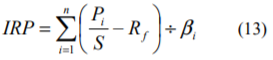
各企業の株式のインプライド・リスクプレミアムは、その株式の時価総額が小さい(大きい)ほど高く(低く)なる傾向があります。また、加重平均に際しては、時価総額の小さい(大きい)株式の組み入れ割合が低く(高く)なります。その結果、加重平均型のインプライド・リスクプレミアムは、全ての企業の株式を同じ比重で組み入れる単純平均型のインプライド・リスクプレミアムよりも低くなります。

3. 2 サイズ・リスクプレミアム

加重平均型のサイズ・リスクプレミアムを求めるにあたっては、(10)式で表されていた全株式のボラティリティの平均値σmを、株式時価総額に基づく加重平均とします。

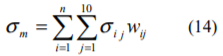
ここでwijは、第j階級に属するある企業の株式の時価総額が、集計対象となった全株式の時価総額に占める割合であり、次式により示されます。

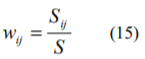
また、階級別の超過収益率の平均値を求めるにあたっては、その階級に含まれる各企業の時価総額が、その階級の時価総額全体に占める割合を用いて、各企業のボラティリティを加重平均します。

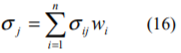
ここで、σjは第j階級に属する全株式のボラティリティの平均値です。wiは、第j階級の時価総額に占める、ある株式の時価総額の割合であり、次式により示されます。

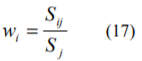
ここで、Sjは第j階級に属する全株式の時価総額です。以上の前提を置いた場合、(9)式のサイズ・リスクプレミアムは次式のように修正されます。

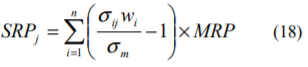
(18)式から明らかなように、加重平均型のサイズ・リスクプレミアムもマーケット・リスクプレミアムに比例します。また、ある階級のボラティリティの加重平均値が、市場全体のボラティリティの加重平均値より低くなる場合には、サイズ・リスクプレミアムが負となることもあります。
さらに、加重平均型のサイズ・リスクプレミアムでは、全階級のサイズ・リスクプレミアムの加重平均値が0となります。すなわち、(18)式で示されるサイズ・リスクプレミアムを全ての階級について加重平均すると次式のようになります。

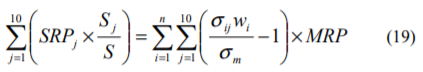
ここで、(15)式と(17)式の関係を利用すると、wiを次式で表すことができます。

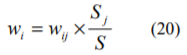
(20)式の関係を用いて(19)式からwiを消去すると次式のようになります。

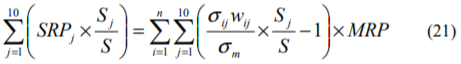
(14)式の関係を利用し、(21)式からσijwijを消去すると次式のようになります。

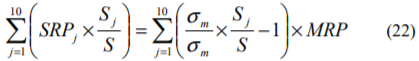
さらに、全階級の時価総額の合計はSとなるため、(22)式を以下のように表すことができます。

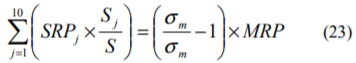
右辺の括弧内が0となるため、全階級のサイズ・リスクプレミアムの加重平均が0となることが確かめられました。

4. 株主資本コストの推計結果に及ぼす影響

3. 1で述べた通り、時価総額の大きい株式をより高い比重で組み入れる加重平均型のインプライド・リスクプレミアムは、全ての企業の株式を同じ比重で組み入れる単純平均型のインプライド・リスクプレミアムよりも低くなると考えられます。以下では、平成26年1月時点のマーケット・リスクプレミアム及びサイズ・リスクプレミアムの前提となったデータを用いて、加重平均型のリスクプレミアムを算出し、算定される株主資本コストにどの程度の影響が生じるか検討します。

4. 1 インプライド・リスクプレミアム

平成25年10月時点において、集計対象となった全企業のインプライド・リスクプレミアムの単純平均値は8.37%でした。これに対し、同一の企業を対象として株式時価総額で加重平均した値は6.81%と算定されます。

4. 2 サイズ・リスクプレミアム

表1は、平成25年10月に集計された単純平均型のサイズ・リスクプレミアムを示したものです。前提となるマーケット・リスクプレミアムの水準は、4%から9%の範囲で0.5%刻みに設定するほか、その時点の単純平均型インプライド・リスクプレミアムであった8.37%と、上記で算出された加重平均型インプライド・リスクプレミアム6.81%を想定し、それぞれに対応するサイズ・リスクプレミアムを示しています。

＜表1 単純平均型のサイズ・リスクプレミアム＞

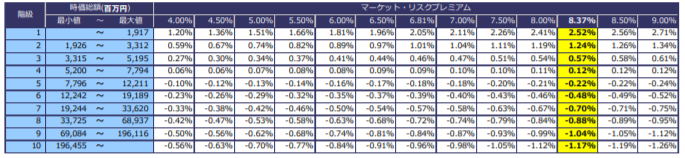
これに対し、表2は、各階級の超過収益率の算出に際し、単純平均に代えて時価総額で加重平均した場合の結果を示したものです。

＜表2 加重平均型のサイズ・リスクプレミアム＞

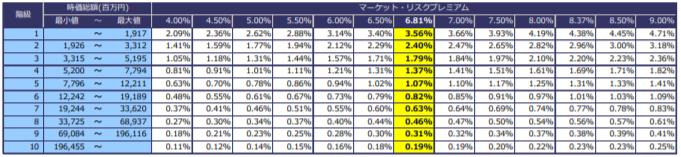
表1と表2を対比すると、以下の二点において違いが生じていることが分かります。

4. 2. 1 マーケット・リスクプレミアム1単位当たりのサイズ・リスクプレミアムの水準

第1階級を前提とした場合、単純平均型ではマーケット・リスクプレミアム1%あたり約30%のサイズ・リスクプレミアムが生じますたが、加重平均型では約52%となります。すなわち、加重平均型を前提とした場合の方が、株式時価総額の小さい階級に対し、より高い超過収益率が要求される結果となります。これは、各階級のサイズ・リスクプレミアムの加重平均が0になるという3. 2で示した性質上、加重平均値に対してより小さな影響しか及ぼさない株式時価総額の低い階級のサイズ・リスクプレミアムは、単純平均型に比べて必然的に高くなるためです。

4. 2. 2 サイズ・リスクプレミアムが生じる階級の数

単純平均型では、第5階級以上はプレミアムでなくディスカウントが生じていたのに対し、加重平均型では全ての階級にプレミアムが生じています。
ここで、各階級のサイズ・リスクプレミアムの加重平均が0になるという性質を考慮すると、理論上少なくとも一つの階級、すなわち株式時価総額が最も大きい階級については、プレミアムではなくディスカウントが生じると考えられます。それにもかかわらず、全ての階級にプレミアムが生じているのは、実際の集計に際し、階級の推移に伴うサイズ・リスクプレミアムの変動を平準化する目的で、算出された各階級の超過収益率の平均値に対して近似曲線を当てはめており、当該曲線による近似値と、実際の超過収益率との間に若干の差異が生じるためです。
このように、株式時価総額が最も大きい階級においては、推計手法の関係上、理論的に予想されるのとは異なる結果が生じていますが、当該階級以外全てプレミアムが発生するという現象は、単純平均型に対する加重平均型の特徴の一つです。

4. 3 株主資本コストの推計結果に及ぼす影響

4. 2. 1で述べた通り、単純平均型ではマーケット・リスクプレミアム1%当たり約30%であったサイズ・リスクプレミアムが、加重平均型では約52%に上昇することから、株主資本コストには相当程度の影響が生じるとも思われます。しかしながら、加重平均型を前提とした場合には、インプライド・リスクプレミアムが低下することを4. 1で示しました。したがって、単純平均型と加重平均型の相違が株主資本コストに及ぼす影響を検討するには、マーケット・リスクプレミアム及びサイズ・リスクプレミアムの算出方法を、単純平均型と加重平均型のいずれか一方に統一するのが整合的です。
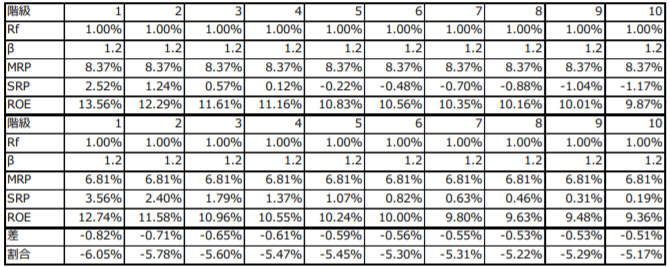
表3-1及び3-2は、表1及び2に示した各手法に基づくサイズ・リスクプレミアムを前提として、株主資本コストの計算例を示したものです。各表の上段には単純平均型のインプライド・リスクプレミアム及びサイズ・リスクプレミアムを前提とした株主資本コストの算定結果が、中段には加重平均型のインプライド・リスクプレミアム及びサイズ・リスクプレミアムを前提とした株主資本コストの算定結果が示されており、下段には両手法に基づく算定結果の差が示されています。リスクフリーレートはいずれの場合も1%とし、βは表3-1では0.8, 表3-2では1.2としました。
たとえば表3-1において、第1階級に着目した場合、株主資本コストは単純平均型では10.22%, 加重平均型では10.01%と算定されます。よって、株主資本コストは加重平均型によった方が単純平均型より低くなり、絶対水準では0.21%, 相対比では2.05%の差が生じます。また、第10階級に着目すると、単純平均型と加重平均型による算定結果の差は絶対水準で0.11%, 相対比で1.69%となります。したがって、最終的に算定される株主資本コストの水準は、単純平均型でも加重平均型でもおおむね一致することが分かります。βを1.2に設定した表3-2では、相対比にして最大6.05%の差が生じてはいるものの、依然として合理的な範囲の変動と考えることもできます。

＜表3-1 株主資本コストの推計結果：βが0.8の場合＞

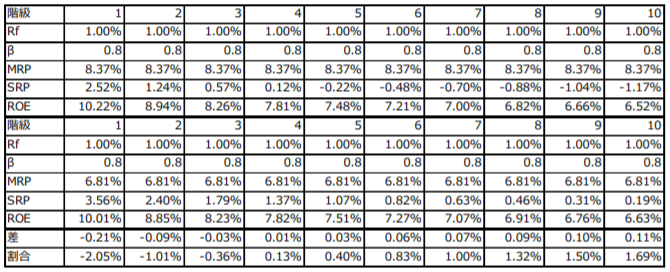
＜表3-2 株主資本コストの推計結果：βが1.2の場合＞

5. おわりに

株式価値算定の実務においては、複数の評価手法を併用し、それらに基づく評価結果を相互に参照することで、それぞれの手法における前提条件の妥当性を検証することが有益とされています。すなわち、複数の評価手法による結果に著しい相違が生じた場合、いずれか一方あるいは双方の前提条件が適切でない可能性が疑われるところ、差異の原因を検証・吟味することによって、より合理的な評価結果が導かれる可能性が高まるということです。本稿において、インプライド・リスクプレミアム及びサイズ・リスクプレミアムに対し、従来の単純平均型に加えて加重平均型の概念を導入し、それぞれに基づく株主資本コストの推計結果を比較検討する試みは、そのような相互参照の効果を企図したものであり、これにより一定程度の合理性は確かめられたものと考えています。

以上

Tweet

Pocket