サイズ・リスクプレミアム再考–ヒストリカル手法とインプライド手法-｜企業価値評価・算定のプルータス・コンサルティング公式サイト

1. はじめに

弊社では、平成21年1月から企業価値評価用データ配信サービス”Value Pro”の提供を開始し、株主資本コストの推計に必要となるβ及びリスクプレミアムを集計、配信してきました。中でも、本サービス独自のデータとして、インプライド手法に基づきマーケット・リスクプレミアムを推計したインプライド・リスクプレミアムと、国内市場のデータに基づくサイズ・リスクプレミアムが挙げられます。
ここで、インプライド手法とは、現在の市場において観察されるデータから、目的となる指標を逆算する手法をいいます。これに対し、過去の長期間のデータを平均する手法をヒストリカル手法といいます。
本サービスでも、マーケット・リスクプレミアムについてはそれぞれの手法に基づくデータを提供しています。すなわち、過去の長期間の超過収益率を平均することにより算出されるのがヒストリカル・リスクプレミアムであり、企業の予想利益と株価の関係から逆算されるのがインプライド・リスクプレミアムです。
これに対し、サイズ・リスクプレミアムとしては、ヒストリカル手法に基づくものが存在せず、インプライド手法に準じて推計されたデータのみの提供となっています。本稿では、サイズ・リスクプレミアムの推計に際してのヒストリカル手法の考え方を紹介した上で、本サービスで提供しているサイズ・リスクプレミアムの考え方及び算出方法を示し、ヒストリカル手法との相違を明らかにします。

2. サイズ・リスクプレミアムとは

サイズ・リスクプレミアムとは、株主資本コストの推計に際し、規模が小さい企業に対して適用される追加的なリスクプレミアムをいいます。最も一般的な推計モデルである資本資産評価モデル(CAPM)を前提とした場合、サイズ・リスクプレミアムは以下のような形で適用されるのが一般的です。

(1)式の左辺は、ある株式のリスクフリーレートに対する超過収益率の期待値、βiはマーケット・リスクプレミアムの変動に対する当該株式の感応度、MRPはマーケット・リスクプレミアム、SRPはサイズ・リスクプレミアムです。本来のCAPMでは、βとマーケット・リスクプレミアムのみにより超過収益率が推計されるのに対し、サイズ・リスクプレミアムを考慮する場合には、追加的なリスクプレミアムが加算されます。
サイズ・リスクプレミアムが発生する理由としては、小規模な企業のリスクが大規模な企業のリスクよりも高く、したがって投資家がより高い収益率を期待するからという説明がなされることがあります。しかし、後述する通り、小規模な企業のリスクが相対的に高いのは事実ですが、超過収益率の水準は必ずしもリスクの水準に比例するものではありません。少なくともCAPMの理論においては、マーケット・リスクプレミアムに加えて追加的なリスクプレミアムを考慮する必要はないとされています。

3. CAPMにおけるリスクプレミアムの考え方

上記の通り、CAPMにおいてはマーケット・リスクプレミアムが唯一のリスクプレミアムとされます。以下では、このような結論が導かれる理由を明らかにします。

3. 1 期待収益率の前提となるリスクとは

CAPMにおいては、投資家は危険回避的との前提が設けられます。危険回避的とは、期待収益率が一定ならばよりリスクの低い投資機会を選好するという投資家の態度をいいます。ここで、リスクは次式で示されるボラティリティにより定量化されます。

(2)式の通り、ボラティリティとは、ある株式の収益率の標準偏差に他なりません。収益率の観察値uiが平均値の回りに集中するほどボラティリティは低くなり、uiが大きく変動するほどボラティリティは高くなります。
ただし、ボラティリティがリスクの尺度となるのは、単一の株式に投資する場合に限られます。複数の株式に投資する場合は、ある株式の収益率が正であっても、その他の株式の収益率が負となる場合が生じるため、それらを組み入れたポートフォリオのボラティリティは、それぞれの株式へ別個に投資した場合のボラティリティの平均値よりも小さくなるからです。これをポートフォリオのリスク分散効果といいます。

3. 2 CAPMの前提となるリスクとは

分散投資を前提に、リスクの内容を再構成したのがCAPMです。CAPMにおいては、投資家が多数の株式に対する分散投資を通じてリスクの最小化を図ることにより、均衡状態としての市場ポートフォリオが形成されるとの前提が置かれます。
市場ポートフォリオにおいては、特定の株式に固有のリスクは減殺され、景気、金利、為替など、市場全体に影響を及ぼすリスクだけが投資家の考慮すべきリスクとなります。ここで、ボラティリティで記述されるリスクをトータルリスクといい、そのうち分散投資によって減殺可能な個別のリスクをアンシステマティック・リスク、分散によっても回避できない共通のリスクをシステマティック・リスクといいます。
また、市場ポートフォリオの超過収益率をマーケット・リスクプレミアムといいます。市場ポートフォリオに組み込まれた個々の株式の超過収益率は、マーケット・リスクプレミアムに対し、その株式の感応度βを乗じることにより算定されます。このような関係を示したのが次式であり、これは(1)式からサイズ・リスクプレミアムを除いたものに他なりません。

ただし、(3)式における変数には、個々の株式及び市場ポートフォリオの収益率の期待値が含まれており、これらを直接観察することはできません。そこで、実際の分析においては、次式のようなモデルを構築し、実際の市場において観察されたデータから回帰分析によりβを推計します。

ここでRit-Rftはt期における超過収益率、αiは回帰式の切片です。Rmt-Rftは、概念的にはt期における市場ポートフォリオの超過収益率を用いるべきですが、市場ポートフォリオの超過収益率を直接観察することはできないため、通常は流動性の高い市場の株価指数の収益率から無リスク金利を控除した値を用います。また、eitは誤差項であり、回帰式では説明できない超過収益率の変動を意味しています。
(4)式のモデルにより推計されたβは、形式上次式のように表すことができます。

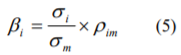
σmは、 (2)式に準じて求めた市場ポートフォリオのボラティリティであり、ρimはある株式と市場ポートフォリオの価格変動の相関係数です。ただし、上記と同様の理由により、実際の分析においては、直接観察できない市場ポートフォリオの変動に代えて、十分に分散された市場の株価指数を用います。また、相関係数は、二つの変数の相関性を示す指標で、両者が全く無関係に変動する場合は0を、完全に連動する場合は絶対値で1をとり、通常は絶対値で0から1の間をとります。
(5)式は、ある株式のβが、その株式のトータルリスクのみならず、市場ポートフォリオとの相関性にも依存することを示しています。すなわち、トータルリスクが高くとも、市場ポートフォリオとの相関性が低い株式では、βが市場全体の平均より低くなるという現象が生じ、逆の現象も生じ得ます。
したがって、CAPMを前提とする限り、小規模な企業だからといってβが高いとは限らず、推計される超過収益率が高くなるとは限りません。むしろ、小規模企業の株価変動が市場ポートフォリオに及ぼす影響は無視しうるほど小さいため、一定の影響力を有する大規模企業に比べて、βは低くなる傾向があります。よって、CAPMの理論的な枠組の中では、サイズ・リスクプレミアムが発生する余地はありません。

4. サイズ・リスクプレミアムを説明するための理論構成

上記の結論にもかかわらず、CAPMで推計された資本コストに対し、サイズ・リスクプレミアムを加算する実務が散見される理由として、最も広く認知されているのが小型株効果です。小型株効果とは、時価総額の小さい株式に、CAPMで推計される理論値よりも高い収益率が観察されるという現象をいいます。以下では、小型株効果を前提としたサイズ・リスクプレミアムの考え方と、その限界について明らかにします。

4. 1 小型株効果を反映したサイズ・リスクプレミアムの定量化：ヒストリカル手法

小型株効果を資本コストに反映するにあたっては、ヒストリカル手法に基づくサイズ・リスクプレミアムが用いられます。すなわち、株式市場に属する企業をいくつかの時価総額階級に分け、それぞれの階級について過去一定期間における実際の収益率の平均値を求め、CAPMに基づき推計される当該階級の収益率を控除することにより、その階級のサイズ・リスクプレミアムが次式のように算定されます。

SRPjはある時価総額階級のサイズ・リスクプレミアムです。またRjは過去一定期間におけるその階級の収益率の平均値、MRPはその時価総額階級が属する市場のマーケット・リスクプレミアムです。

4. 2 サイズ・リスクプレミアムの算定におけるヒストリカル手法の問題点

ヒストリカル手法に基づくサイズ・リスクプレミアムの定量化は、小型株効果という広く認知された現象を背景としており、実際の推計式も(6)式の通りきわめて単純です。しかし、実務で適用するにあたっては、次のような問題点があります。

4. 2. 1 データの入手が容易でないこと

ヒストリカル手法の適用にあたっては、短期的な変動の影響を平準化した長期的な水準を求めるため、一定以上の期間にわたるデータを用いる必要があります。しかし、我が国においては、米国と異なり、株式市場を時価総額階級別に細分化した長期間の時系列データが存在しません。

4. 2. 2 特定市場のマーケット・リスクプレミアムに依存すること

(6)式で定義した通り、ヒストリカル手法に基づくサイズ・リスクプレミアムは、ある時価総額階級について、過去一定期間における実際の収益率の平均値を求め、CAPMに基づき推計される当該階級の収益率を控除することにより算定されます。そして、CAPMに基づく推計値の算出にあたっては、その時価総額階級が属する株式市場のマーケット・リスクプレミアムの水準が前提となります。よって、前提となる市場が変われば、サイズ・リスクプレミアムも変動しうるのであり、他国の市場において観察されたサイズ・リスクプレミアムを用いた場合、その合理性は大きく減じられてしまいます。

4. 2. 3 観察期間の長短に依存すること

ヒストリカル手法に共通する問題点として、観察期間の長短に応じて算定結果が大きく変動する点が挙げられます。

4. 2. 4 小型株効果の存在に関し議論の余地があること

小型株効果は、我が国の市場においては明確には観察されておらず、米国市場においても1980年代以降ほとんど観察されなくなったとする見解があります。
表は、米国市場において、小型株の収益率から大型株の収益率を控除することにより算定されるSMB(Small Minus Big)と呼ばれる指標を、一定期間について平均したものです¹⁾ダートマス大学のKeneth French教授がCenter for Reserch in Security Pricesのデータベースに基づき集計した年次収益率の単純平均によっています。 。SMBが正の場合には、小型株効果の存在を推定することができます。しかしながら、下記の表からは、1940年頃までほとんど観察されなかった小型株効果が、1980年頃にかけて顕在化したものの、その後現在までの期間においては、再び不明確となっていることが分かります。

＜表 米国におけるSMBの推移＞

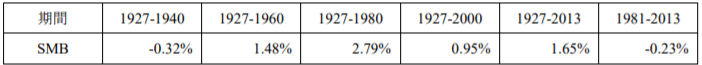
4. 2. 5 理論的根拠の乏しさ
ヒストリカル手法に基づくサイズ・リスクプレミアムは、実際に観察された収益率が投資家の期待収益率を正しく示しており、CAPMに基づく推計値は期待収益率を正しく反映していないとの暗黙の前提を置いています。その点では、実績値と理論値の差として事後的に把握されるものにすぎず、CAPMと異なり明確な理論的背景を有していないという限界があります。

5. プルータス・コンサルティングの考えるサイズ・リスクプレミアム

以上の通り、ヒストリカル手法に基づくサイズ・リスクプレミアムは、我が国の実務で適用するにあたってはいくつかの重要な問題点を有しています。そこで、Value Proでは代替的な手法を採用しています。

5. 1 基本的な考え方

「小規模企業は大規模企業よりもリスクが高い」という考え方については、おそらく異論がないでしょう。しかしながら、CAPMの理論においては、ボラティリティの高い株式でも、市場ポートフォリオとの相関性が低い場合には、リスク分散効果により減殺されるリスクが大きいため、結果として資本コストは低くなり、サイズ・リスクプレミアムが発生する余地はありません。
そこで、Value Proでは、CAPMとは異なる観点から、収益率がボラティリティに比例するとの仮定に基づき、各時価総額階級の超過収益率を算定します。サイズ・リスクプレミアムは、上記により算定された時価総額階級別の超過収益率から、市場全体の超過収益率であるマーケット・リスクプレミアムを控除することにより算定されます。
このようにValue Proのサイズ・リスクプレミアムは、投資家の期待収益率がCAPMに基づき推計されることを前提としつつも、小型株については、ボラティリティの高さに応じた追加的な収益率を投資家が要求するとの仮定に基づいています。また、集計にあたっては、長期間の時系列データの平均値に依存せず、現在時点におけるボラティリティに基づき推計されるという点で、インプライド手法に準ずる方法といえます。

5. 2 サイズ・リスクプレミアムの算出過程

Value Proのサイズ・リスクプレミアムは、以下の3段階を経て算出されます。

5. 2. 1 各企業の超過収益率の算出

ある株式の超過収益率が、次式のように表されるものと仮定します。

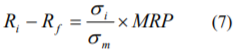
(7)式は、ある株式の超過収益率が、当該株式のボラティリティに比例することを意味しています。(7)式は、CAPMに基づく超過収益率を示した(3)式において、右辺のβをボラティリティの比に置き換えたものに他なりません。(7)式の右辺に含まれるボラティリティの比は、(5)で示されるβから、相関係数を除いたものです。
よって、(7)式は、CAPMに基づく超過収益率の推計式から、ポートフォリオのリスク分散効果を除いたものと位置づけることができます。そのため、ボラティリティの比の分子となるσmには、株価指数ではなく、前提とする市場に存在する企業のボラティリティの平均値を用います。株価指数の変動には、ポートフォリオのリスク分散効果が反映されているからです。

5. 2. 2 各階級の超過収益率の算出

我が国の株式市場に上場している国内企業を、時価総額別を基準として10階級に分け、各階級に属する企業の超過収益率を平均することにより、次式のようにそれぞれの階級の超過収益率を算出します。

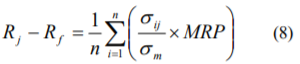
ここで、Rj-Rfは第j階級の超過収益率、nは各階級に属する企業の数、σijは第j階級に属する企業のボラティリティを意味します。小型株のボラティリティは大型株に比べて一般に高いため、時価総額の低い階級では、(8)式を前提とした超過収益率も相対的に高くなります。

5. 2. 3 サイズ・リスクプレミアムの算出

(8)式で算定されたある階級の超過収益率の平均値から、前提となったマーケット・リスクプレミアムを差し引くことにより、その階級のサイズ・リスクプレミアムが算出されます。

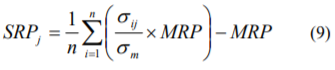
(9)式を整理すると次式のようになります。

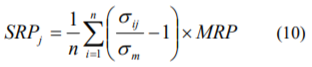
5. 3 Value Proのサイズ・リスクプレミアムの特徴

上記の通り、Value Proのサイズ・リスクプレミアムは、小型株効果を前提としたヒストリカル手法に基づくサイズ・リスクプレミアムとは大きく異なっており、以下のような特徴を有しています。

5. 3. 1 データの入手が容易

(10)式において変数となるのはボラティリティのみであり、我が国の市場における既存のデータのみで算出可能です。

5. 3. 2 特定のマーケット・リスクプレミアムに依存しない

ヒストリカル手法を前提とした(6)式においては、マーケット・リスクプレミアムとしては実際に市場で観察された値を用いる必要がありました。これに対し、(10)式において、マーケット・リスクプレミアムは任意の定数であり、特定のマーケット・リスクプレミアムに依存しません。具体的には、ある階級のボラティリティが、市場全体の平均よりも3割高いとすれば、その階級のサイズ・リスクプレミアムは、マーケット・リスクプレミアムの3割となります。

5. 3. 3 観察期間の長短に依存しない

過去数年間のボラティリティのみを変数とするため、ヒストリカル手法と異なり、観察期間の長短により算定結果が大きく変動することはありません。

6. おわりに

本稿では、小型株効果を前提としたヒストリカル手法に基づくサイズ・リスクプレミアムと、それとは別個の接近法をとるValue Proのサイズ・リスクプレミアムの相違を明らかにしました。
Value Proのサイズ・リスクプレミアムの問題点として、各時価総額階級の超過収益率の算出に際し、制約的な仮定を設けている点が挙げられます。すなわち、各時価総額階級の超過収益率は、当該階級に属する企業のボラティリティに依存し、その結果小型株の超過収益率が相対的に高くなると想定しているところ、我が国においては小型株効果が明確には生じていないとの見解もあります。
とはいえ、実際の収益率に依拠するヒストリカル手法には、本稿で指摘したいくつかの問題点があり、必ずしも万能な手法とはいえません。これに対し、Value Proのサイズ・リスクプレミアムは、「小規模企業は大規模企業よりもリスクが高い」という、大筋で同意を得られるであろう考え方に基づき算出されており、データの入手の容易性、マーケット・リスクプレミアムからの独立性といった取扱いの容易さをも有しています。
株主資本コストの推計に際し、サイズ・リスクプレミアムを考慮する実務がしばしば行われている一方、その前提条件を正しく理解した上で適用している方は、必ずしも多くないのが現状です。本稿が、それぞれの手法の背後にある考え方をご理解いただく一助となれば幸いです。

以上

Tweet

Pocket