回帰分析を応用した国カテゴリ別の相対リスク比率の推計｜企業価値評価・算定のプルータス・コンサルティング公式サイト

1. はじめに

先月発表したNo.72「国カテゴリを基準とした相対リスク比率の推計」では、各国市場の株価変動性を、主として信用リスクに基づいたカテゴリ別に平均した場合、高い信用リスクに対応するカテゴリほど、最も信用リスクの低いカテゴリに対する相対的な株価変動性、すなわち相対リスク比率も高くなる傾向があることを示しました。また、単一市場を対象とした場合には顕著であった相対リスク比率の時系列変化が、カテゴリ別の集計により安定化することも明らかにしました。
しかしながら、国カテゴリ別に集計した場合でも、信用リスクの高いカテゴリの相対リスク比率が、信用リスクの低いカテゴリのそれを下回るという現象が、一部の時点、カテゴリについて生じました。本稿では、このような直観に合致しない結果を排除し、相対リスク比率の分析結果をより簡明なものとする目的で、回帰分析の手法を応用した推計を行います。

2. 回帰分析の概要

回帰分析とは、ある変数が他の変数に影響を及ぼすとき、両者の間の関係式を導くための手法です。このとき、影響を及ぼす変数を説明変数、影響を受ける変数を被説明変数といいます。以下では、本稿の分析をご理解いただくのに最低限必要な回帰分析の考え方を概説します。
なお、No.62「株価分析の一手法としての回帰分析」では、より詳細な解説をしておりますので、興味を持たれた方はそちらを併せてご覧いただければ幸いです。

2. 1 回帰分析の一例

たとえば、株価指数が上昇しているときは、それを構成する個々の企業の株価も全体として上昇傾向にあると考えられます。ただし、全ての企業の株価が株価指数と同じ割合で上昇するとは限らず、株価指数の変動に対して顕著に反応する銘柄もあれば、そうでない銘柄もあります。そこで、株価指数の変動率を説明変数、個々の株価の変動率を被説明変数として、以下のような関係式が成り立つと仮定します。

ここでRiはある企業の株価変動率、Rmは株価指数の変動率であり、αとβはそれぞれ定数項、回帰係数と呼ばれます。[1]式は、Rmを横軸、Riを縦軸とした場合の、切片がαで傾きがβの直線を表しています。この関係式は、株価指数が1単位変化したとき、ある企業の株価がβだけ変動することを意味しています。つまり[1]式のβは、株主資本コストの推計モデルである資本資産評価モデル(CAPM)におけるβに相当します。

2. 2 最小二乗法による推定
実際の推計においては、複数時点の株価指数及び株価の変動を観察し、以下のようなモデルを作成します。

ここで添字のtは時点を示しています。またutは誤差項と呼ばれる変数です。誤差項を想定するのは、株価指数と株価の変動率を複数時点にわたって観察した場合、それらが一直線上に並ぶとは限らないからです。
図1は、No.62「株価分析の一手法としての回帰分析」に掲載した、TOPIXの変動率を横軸、株式会社日立製作所の株価変動率を縦軸にとり、平成26年1月1日から6月30日までの各営業日の変動を座標面上に描いたグラフです。

＜図1日立製作所の株価変動の回帰式＞

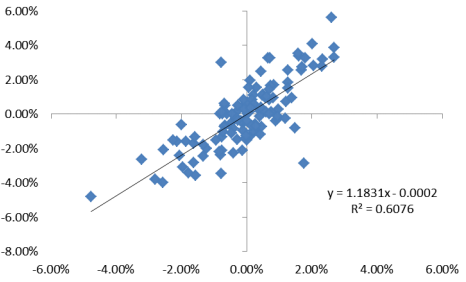
図からも明らかなように、TOPIXの変動率が正(負)の場合は株価の変動率も正(負)となる傾向があり、またTOPIXの変動率が大きい(小さい)ほど株価の変動率も大きく(小さく)なる傾向が窺われます。そこで、具体的にどの程度大きく(小さく)なるかを推定したのが図中の直線です。この直線は、回帰分析により導かれる直線であることから回帰直線と呼ばれます。
回帰直線の推定方法には様々なものがありますが、最も基本となるのは最小二乗法です。最小二乗法とは、座標面上に散らばる点から直線までの距離を最小化するように、直線の切片と定数項を決める方法です。実際の計算は、[2]式のutを全ての時点について二乗した合計を最小化することにより行われます。
その結果導出された関係式が図1に示されています。この式は、TOPIXが1単位変動したとき、日立製作所の株価は約1.18単位変動することを意味します。
また、式の下に示されたR2は決定係数と呼ばれる指標で、日立製作所の株価変動の約60%がTOPIXの変動により説明可能であることを意味しています。座標面上に散らばる点が直線状に近くなればなるほど決定係数は1に近付き、推定された回帰直線の説明力は高くなります。ただし、変数間の関係性は様々であり、決定係数がどの程度であれば十分説明力があるといえるかどうかについては一概にいえません。たとえば株価は、株価指数の変動のみならず、個々の企業が直面している様々な環境の影響を受けるため、0.6を超える決定係数は十分に高い部類に属します。

3. 相対リスク比率推計への応用

以下では、No.69「国カテゴリを基準とした相対リスク比率の推計」で示した国カテゴリを説明変数、国カテゴリ別の相対リスク比率を被説明変数として、回帰分析により両者の関係式を求めます。

3. 1 国カテゴリとボラティリティの関係

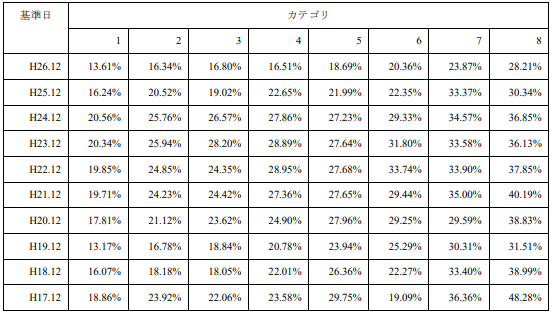
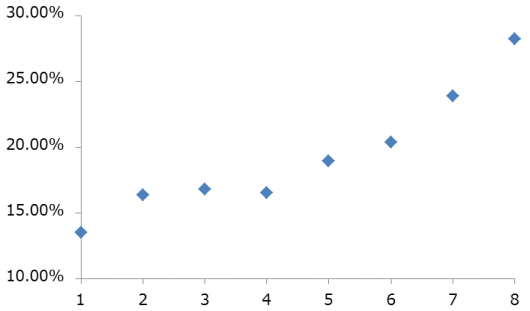
表1は、No.69に掲載した、平成17年から平成26年までの各年末における国カテゴリ別の平均ボラティリティを示したものです。また図2は、国カテゴリを横軸に、各カテゴリのボラティリティの平均値を縦軸にとり、平成26年末のデータを座標面に描いたものです。
各カテゴリの平均ボラティリティを示す点を線で結ぶと、全体を通じてみればおおむね右上がりではあるものの、カテゴリ2から4にかけてほぼ横ばいとなり、その後再び上昇に転じるという、三次曲線に近い変化をしていることが分かります。このことからすると、カテゴリと平均ボラティリティの関係を回帰分析により最も適切に近似するには、三次式を用いればよさそうです。しかし、国カテゴリ別のリスクを定量化するという分析の目的からすれば、上昇してから低下して再び上昇する三次式よりも、カテゴリが1から8へ推移するに従って単調に増加するものとして取り扱う方が簡明です。とはいえ、単純に直線を当てはめても、曲線に近い形を示すデータの動きを適切に近似できない可能性があります。そこで、以下では最も基本的な直線による近似と、より精度が高いと思われる指数近似による回帰分析を試みます。

＜表1 国カテゴリ別の平均ボラティリティ＞

＜図2 国カテゴリとボラティリティの関係＞

3. 2 直線による近似

2. 2 で示したのと同様に、被説明変数と説明変数の関係を回帰直線により近似します。

3. 2. 1定式化

回帰直線は、以下の式に実際のデータを代入し、utの二乗和を最小化することにより推定されます。ここでσiはi番目のカテゴリの平均ボラティリティ、Categoryiはi番目のカテゴリの番号、uiは座標面上の点と直線との差を示します。

3. 2. 2 回帰式の推定

回帰直線の推定結果は図3に示した通りです。

＜図3 推定された回帰直線＞

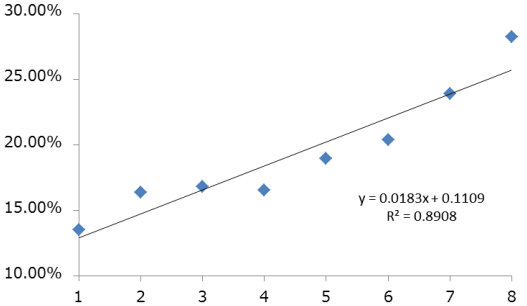
図中の回帰直線は、国カテゴリの番号が1つ増えると、それに応じて約平均ボラティリティが約1.83%高くなることを示しています。
たとえば、第1カテゴリのボラティリティは、図中の関係式のxに1を代入することにより、約12.91%と推定され、第8カテゴリについては同様に約25.72%と推定されます。実際の値はそれぞれ13.61%と28.21%であり、特に第8カテゴリについては実際の値と推定値の差が広がってはいるものの、それでも割合にすれば10%に満たない誤差です。決定係数が0.8908であることからも、単純な直線であっても国カテゴリとボラティリティの関係の大半を説明できていることが分かります。

3. 2. 3 各年におけるボラティリティの推定

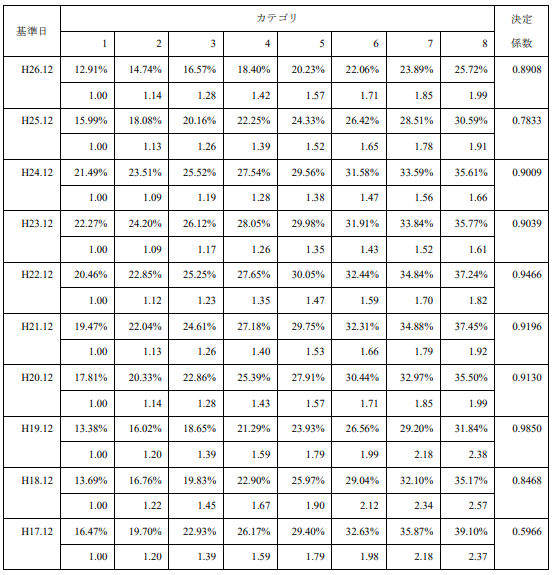
表2は、平成17年から平成26年の各年末につき、国カテゴリとボラティリティの関係を直線により近似したものです。また、推定された回帰式の決定係数も併せて示しました。

＜表2 直線近似による推定ボラティリティ＞

3. 3 指数関数による近似

3. 2で示した通り、単純に直線を当てはめた場合でも、国カテゴリと平均ボラティリティの関係を良好に近似することができました。しかし、全体としては曲線状にも見える関係に直線を当てはめることによって、特に第8カテゴリでは実際の値と推定値の開きが大きくなっています。
図2に示したような関係をより適切に近似するには、指数関数を用いることが考えられます。指数関数は、単調に増加しつつも、増加の割合が次第に大きくなっていく性質を有することから、直線による近似に比べ、前半(後半)のカテゴリでは推定値が低く(高く)なる傾向を有します。

3. 3. 1 定式化

国カテゴリとボラティリティの関係を指数関数により記述する場合には、以下の関係式を用います。

ここでσiはi番目のカテゴリの平均ボラティリティ、Categoryiはi番目のカテゴリの番号、αは定数、βは回帰係数、eはネイピア数と呼ばれる自然対数の底です。
図2に示した国カテゴリとボラティリティの関係を指数曲線により近似する場合、単調に増加し、なおかつ増加率が逓増する指数曲線が適合すると考えられます。この場合、αは1より大きい値を、βは正の値をとることが予想されます。
最小二乗法を適用するには、変数間に直線的な関係が存在している必要があり、指数曲線を最小二乗法により直接推定することはできません。そこで、[3]式の両辺の対数をとることにより、以下の関係式を導きます。

3. 3. 2 回帰式の推定

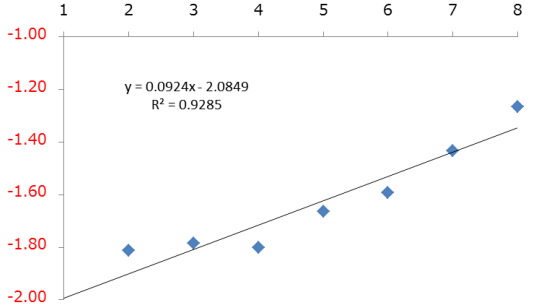
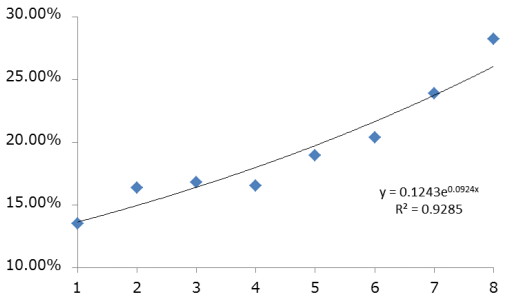
図4は、[4]式により表される回帰直線の推定結果を示したものです。また、図4の縦軸にとられているボラティリティの対数を元に戻すことにより指数曲線を描くことができ、これを示したのが図5です。それぞれの図中に示した通り、決定係数は0.9285で、直線により近似した場合の0.8908を上回ることから、モデルの説明力は向上したことが分かります。
各カテゴリのボラティリティの推定値は、図5中の式のxにカテゴリの番号を当てはめることによって算出できますが、指数関数を用いるため、一般の電卓では直接計算できず、Excelなどのアプリケーションまたは関数電卓を用いる必要があります。
Excelを用いる場合には、Exp関数にeのべき数を代入することにより指数関数の値を求めることができ、これに定数を掛け合わせたものがボラティリティの推定値となります。第8カテゴリのボラティリティの推定値は、以下の通り26.04%です。

＜図4 推定された回帰直線＞

＜図5 推定された指数曲線＞

3. 3. 3 各年におけるボラティリティの推定

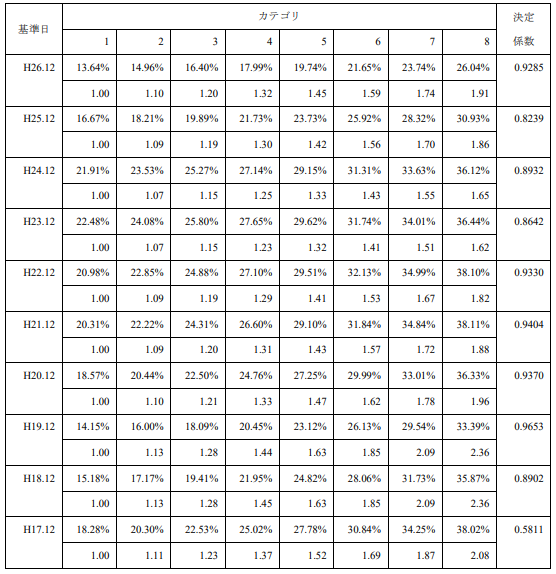
表3は、平成17年から平成26年の各年末につき、国カテゴリとボラティリティの関係を直線により近似したものです。また、推定された回帰式の決定係数も併せて示しました。
平成26年12月時点については、直線近似の場合に比べ決定係数が上昇するものの、平成17年、平成19年、平成22年、平成23年、平成24年の各年については、逆に決定係数が下がっています。つまり、集計対象とした10年のうち、決定係数が上昇した年と下落した年が半々ということです。この事実から判断する限り、指数曲線による近似が直線による近似に対して明らかに優位性を持つとまではいえず、簡明性の観点からは直線近似の方がむしろ妥当といえそうです。

＜表3 指数近似による推定ボラティリティ＞

4. 解決すべき課題

以上の結果、回帰分析を応用することにより、信用リスクが高くなるに従い国カテゴリ別の相対リスク比率も上昇するという関係を、高い精度で近似できることが分かりました。しかしながら、推計された相対リスク比率をどのような形で株主資本コストの推計に適用するかについては、複数の方法が考えられます。次回はその手法について検討する予定です。

以上

Tweet

Pocket